Eev and Maxima
- 1. Display and tex
- 2. `eepitch-maxima'
- 3. Elisp hyperlinks
- 4. Maxima for students
- 4.1. `find-angg-es-links'
- 4.2. Configuring and installing
- 4.3. `M-x ils', `M-x ilq', `M-x ilt', and friends
- 4.4. A first application: [:=]
- 5. Lazy nouns
- 6. Methods
- 7. Embedding in LaTeX
- 7.1. LaTeX instead of TeX
- 8. "Physicist's notation"
- 9. Substitution
- 10. LispTree (and LuaTree)
- 11. Maxima by Example
- 12. Qdraw and myqdraw
- 12.1. Set comprehensions
- 13. `displa_delegate'
- 14. Debugging the Lisp (with Sly)
1. Display and tex
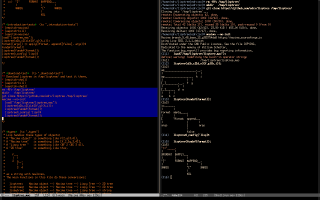
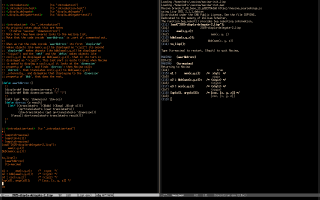
Most of my uses of Maxima nowadays (2025) involve objects that have special "display" and "tex" properties. Here is an example - click to enlarge, and go here to see a page that will be a good introduction to that at some point, but that is far from finished:
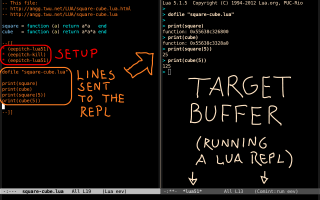
2. `eepitch-maxima'
I use eepitch to send lines from Emacs to Maxima; see the figure below for the main idea, and my presentation at the EmacsConf2021 for the details. The definition of eepitch-maxima in eev is the simplest possible - just this:
(defun eepitch-maxima () (interactive) (eepitch-comint "maxima" "maxima")) |
I tried to write variants that used Fermin MF's maxima-mode instead of just comint, but his maxima-mode behaved in weird ways when it had to send empty lines, and we couldn't fix that easily... so I gave up.
3. Elisp hyperlinks
My notes on Maxima in maxima.e contain lots of elisp hyperlinks like these ones,
(find-maximanode "makelist") (find-maximamsg "37690886 202208 07" "RToy: doc/info/build-html-index.lisp") |
that are htmlized in special ways. They are explained in these other pages: find-maximanode, find-maximamsg.
4. Maxima for students
My presentation at the EmacsConf 2024 was titled "Emacs, eev, and Maxima - Now!", where the "Now!" meant this:
(find-eev2024hsubs "0:42" "so for me this ugly interface ... is much better") (find-eev2024hsubs "8:22" "in less than one hour and even for people") (find-eev2024hsubs "8:25" "who have never seen a terminal in their lives.") |
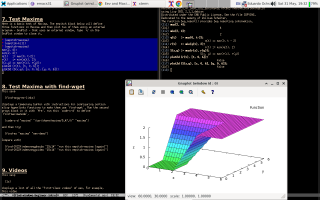
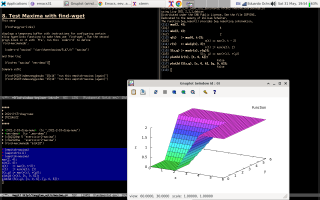
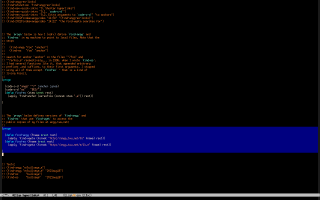
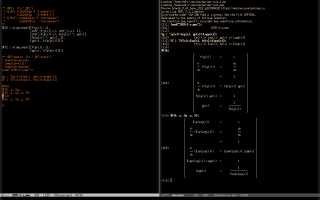
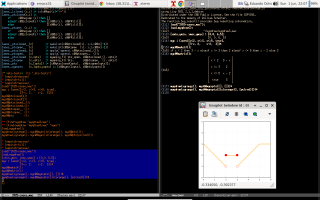
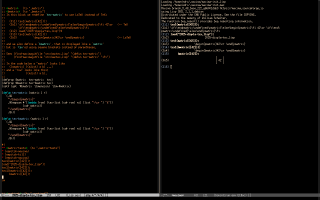
Here's how I'm (sort of) teaching Maxima to these "students who have never seen a terminal in their lives". I start by convincing each of them - each of the interested students; my classes are small - to do a first 5-minute workshop on my laptop in which they run they run the eepitch block in blue in the first screenshot below with `f8's, and they get a Gnuplot window, that they can close with `q'.
Then they do a second 5-minute workshop, in which they first type `M-e' to execute the `(find-es ...)' in the upper left window of the second screenshot above; the `M-e' takes them to a wgetted copy of my notes on Maxima, and to this block,
(find-es "maxima" "eev-demo") |
that contains the eepitch block in blue in the second screenshot, that is very similar to the block in the first screenshot. Then they execute that eepitch block with `f8's and they get the Gnuplot window again. In these two 5-minute workshops they only type `f8's, `q's, and `M-e's, and I do the rest.
Then I start to present to them an eagle-eyed view of what they had just done. They ran the main parts of these two sections of a tutorial - that can also be read in the broser, but in the browser not everything will work...
(find-windows-beginner-intro "7. Test Maxima") (find-windows-beginner-intro "8. Test Maxima with find-wget") |
To run everything locally in their machines they will have to install WSL, Debian, Emacs, eev, and then use eepitch to install some packages. This is explained in these other sections of that tutorial:
(find-windows-beginner-intro "1. Install WSL, Debian, and Emacs") (find-windows-beginner-intro "2. Install eev") (find-windows-beginner-intro "3. Use eepitch to add a Debian repository") (find-windows-beginner-intro "4. Use eepitch to install Debian packages") (find-windows-beginner-intro "5. Use eepitch to install Google Chrome") |
When a student asks for help on our Telegram channel I can usually answer all questions very quickly - I use this "map" to help me answer the harder questions - and we almost always get everything working in about one hour. For most students nowadays asking questions to colleagues is very hard and asking questions to me is beyond impossible, but I solved that problem by just saying, in many occasions and in many places, by both voice and in writing, that I am not a telepath and that students who don't ask questions will be plonked. See:
(find-eev2024hsubs "7:42" "...begged on my knees") (find-eev2024hsubs "8:50" "7. Introduction to plonking") (find-eev2024hsubs "10:15" "8. Plonking and telepathy") |
I have lots of logs of Telegram chats with students who installed everything in about one hour, and that is enough for me.
4.1. `find-angg-es-links'
This is a more technical explanation - recorded in 2022 - of how `find-es' can be redefined to use find-wget.
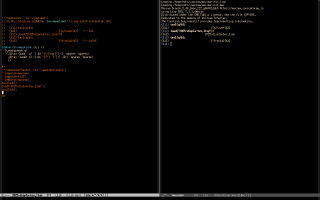
The video below explains a way to run my executable notes on Maxima with eev "without downloading anything extra". When I recorded it I felt that all those ideas were sort of, ahem, revolutionary, and that I had to explain everything in detail... but nowadays I usually suppose that 1) everyone(-ish) will set up `find-es' and `find-angg' to make them use find-wget, and 2) it is better to pretend that the inner details are obvious.
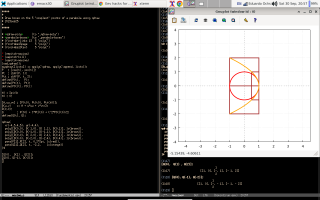
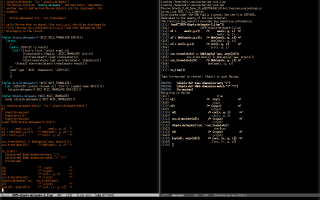
Click on the timestamps below to go to the best points of the (subtitles of the) video. The part that starts at 15:04 shows the demo in the third screenshot.
(find-2022findeevangghsubs "11:29" "make `find-angg' behave in another way") (find-2022findeevangghsubs "14:06" "if we run this we redefine...") (find-2022findeevangghsubs "15:04" "...and searches for this anchor") |
4.2. Configuring and installing
I ask the students to configure Emacs in a certain way - that loads eev on startup, redefines `find-es' and `find-angg' to use find-wget, and does a few things more - and I ask them to install some files for Maxima. The instructions for these steps are here,
(find-windows-beginner-intro "11. Edit your init file") (find-windows-beginner-intro "12. Install qdraw") |
The students start by using Maxima in two ways - that both depend on configuring some things in their "~/.emacs"es
4.3. `M-x ils', `M-x ilq', `M-x ilt', and friends
See:
(find-windows-beginner-intro "12.1. `M-x ils' and friends") |
4.4. A first application: [:=]
I teach Calculus 2 and Calculus 3, and the students are arriving on C2 without knowing how to take a particular case of a formula - which is obviously something that they will have to practice a lot... and now I can show them a screenshot like this,
and send a link like this one in our Telegram channel:
(find-es "maxima" "stewart-pt-p138") |
And then one operation that we use a lot becames less abstract - they see that the [:=] that we use in class can be translated to Maxima using an infix operator "_s_", that is defined here - and they get something that they can practice at home.
5. Lazy nouns
Maxima has a way to make certain operations "less active": for
example, diff(x^3,3) calculates a derivative, but 'diff(x^3,3), with a leading single quote, returns an uncalculated
derivative - see the section about nouns and verbs
in the Maxima manual.
The "noun version" of diff, 'diff, still does some
simplifications - so 'diff is "less active" and diff, but
sometimes I need something that is even less active than that, that
doesn't do any simplifications at all. Here is a quick solution: I
call it "lazy nouns", and it is implemented by creating new symbols,
like _diff, that copy many of the Lisp properties of the original
diff but not the ones that are related to simplifications. The
code is here, and the second screenshot
below shows an application:
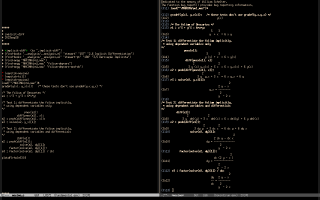
My students in Calculus 2 have so little practice with taking
particular cases that seeing a figure like that, that shows a
demonstration of the formula of the derivative of the inverse function
and its particular case that calculates log', helps them a
lot. The third screenshot is similar, but it shows my favorite way of
convincing people that the formula for integration by substitution
makes sense. Its code is here and it uses dim-antideriv.lisp by Robert Dodier.
6. Methods
Maxima has defstruct, that lets us define "structures", and
"@", that lets us access the fields of structure instances, but it
doesn't come with a built-in way to define methods, or to define
fields whose values are computed dynamically. Here is a quick hack that remedies that; it defines an operation "@@"
that accesses the "methods" of a structure, and that is translated in
this way. If the object o is a structure of kind ab, then:
. defstruct(ab(a, b));
o : new(ab(2, 3));
o@@f (4, 5);
==> ab__f(o, 4, 5);
|
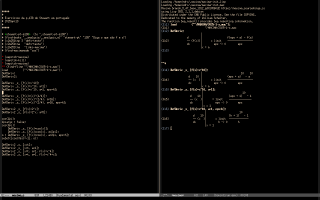
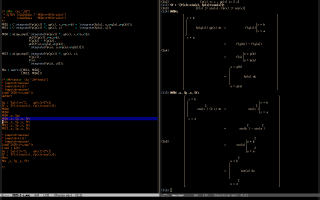
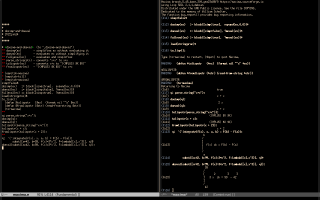
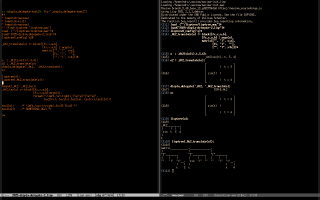
The first screenshot below shows the definition of "@@" and a simple demo:
The second screenshot shows this library, that I use to teach Taylor polynomials to beginners, and that has methods for displaying each of the steps for calculating a Taylor polynomial by hand.
The third screenshot shows this library for functions defined by cases, that uses this syntax,
myc : Cases([x<2, x<=3, x<=5, true],
[3-x, 2, x-2, 3])$
|
and that has:
- a method - `@@makeif' - that generates an `if ... then ... elseif ... else ...',
- a method - `@@matrix' - that displays the function as a table of cases,
- and a family of methods for drawing the function with myqdraw, that "do the right thing" instead of drawing the discontinuities as vertical lines, like `explicit' does.
The fourth screenshot shows this library for (joined) lerps.
7. Embedding in LaTeX
My current way of LaTeXing Maxima code uses Lpeg. Its main module is here, Maxima2.lua, and it produces output like this from this input (plus tweaking). The rest of this section describes an older way.
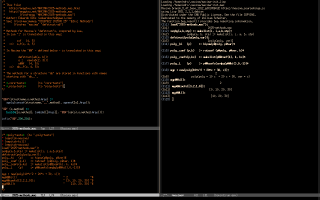
Here is an example of how I am embedding Maxima code in LaTeX files; the trick that makes eepitch ignore a prefix is explained here. If I execute that eepitch block skipping the lines "load" and "display2d" I get a human-friendly output, as in the first screenshot below; if I execute the lines "load" and "display2d" I get an output that I can process with M-x emaxima-conv (that calls emaxima.lua) to obtain this LaTeX code, that becomes this in the PDF. This trick is based on the answers that I got for this question that I sent to Maxima mailing list; note that 1) I am using this copy of emaxima.sty that has two lines commented out, and 2) my emaxima.lua is a quick hack, and it should be converted to elisp at some point.
7.1. LaTeX instead of TeX
By default Maxima generates TeX code that is TeX-y instead of LaTeX-y - for example, if you don't change anything then `tex1(matrix([42]))' returns this:
(%i1) tex1(matrix([42]));
(%o1) \ifx\endpmatrix\undefined\pmatrix{\else\begin{pmatrix}\fi
42\cr
\ifx\endpmatrix\undefined}\else\end{pmatrix}\fi
|
My code that changes that thing with `\ifx's to
\begin{pmatrix}
42\cr
\end{pmatrix}
|
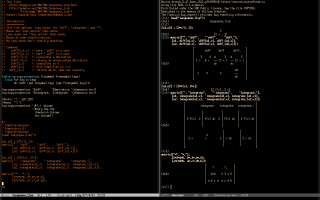
is in 2025-displa-tex.lisp - see the two screenshots below for explanations and tests. Note that I prefer to use backquotes to build lists, and most of the files in the Maxima source prefer to use `append', `cons', and friends... compare my (re)definition of `tex-matrix' with the original definition in src/mactex.lisp.
8. "Physicist's notation"
First version: In 2022jan10 I sent to the Maxima mailing list this big e-mail, that had two parts. In the first part I asked about the (internal) differences between using expressions, like "f : x^2", and using functions, like "g(x) := x^3"; the code associated to that part is here. In the second part I asked if, and how, Maxima supports "physicists' notation" - where "physicists' notation" ("PN") is my informal name for a notation that is common in old books like this one by Silvanus Thompson. In PN variables and functions can share the same names, variables can be "dependent", some arguments can be omitted, and several abbreviations are standard - for example, if y=y(x) then the default meaning for y1 is y1=y(x1)=y(x0+Δx). It turns out that YES, Maxima supports physicists' notation, and it's easy to translate calculations in PN to Maxima if we use gradef and subst in the right way to translate between PN and "mathematician's notation". I recorded a 20s video demo-ing this - it's here, and its code is here. The slides on PN that I prepared for my course on Calculus 3 are here.
Second version (sep/2023): my sample space is small - about 25 people - but apparently in Brazil,
- "all" the "P"ure mathematicians ("group P") treat dependent variables and differentials as abuses of language,
- "all" the "A"pplied mathematicians, physicists and engineers ("group A") treat dependent variables and differentials as something that "everybody knows", and
- no one in either of the two groups knows the exact rules for translating the language of "Calculus with dependent variables and differentials" ("Calculus+") into the language of "Calculus without dependent variables and differentials" ("Calculus-")...
...so "no one" here knows how write an "elaborator", in this sense, that could translate "Calculus+" into "Calculus-". I grew up in Group A and my native language is "Calculus-", but now in my day job I'm teaching integration using books that use "Calculus+", and I thought that the best way to handle my embarassment for not speaking "Calculus+" well enough would be to formalize how that translation can be done.
I'm sort of working on that, and I'm starting by writing some of its functions in Maxima; my functions are here: pn1.mac. That file is a bare prototype at the moment, but to me it feels like the right way to treat dependent variables and differentials as abbreviations. Here is a screenshot:
9. Substitution
My first attempts to understand how Maxima implements the "#$expr$" syntax in Lisp are here: 1, 2, 3. Then Stavros Macrakis explained how I could define "dosimp" and "doeval" and I produced the example below. Its code is here. My long e-mail explaining why I am teaching substitution in this way is here (includes gossip).
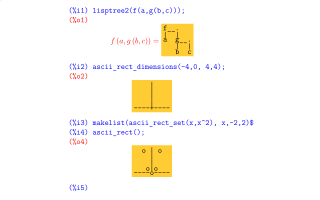
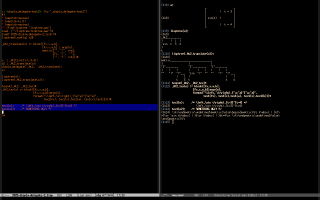
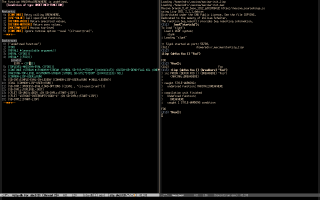
10. LispTree (and LuaTree)
LispTree displays Maxima objects as trees. For example, if we run
* (eepitch-maxima) * (eepitch-kill) * (eepitch-maxima) load("~/lisptree/lisptree.mac") lisptree0_config('lisp)$ lisptree(fundef(format)); lisptree0_config('maxima)$ lisptree(fundef(format)); |
it shows the definition of format as a tree in two different styles:
|
|
Its page is here.
It supersedes LuaTree, that was a quick hack and was hard to install.
If you have eev and Maxima installed then the easiest way to test Lisptree is by running this `find-wgeta',
;; (find-angg "lisptree/lisptree.mac" "download-test") (find-wgeta "https://anggtwu.net/lisptree/lisptree.mac" "download-test") |
that will download a copy of lisptree.mac into a temporary buffer and go to a test block containing this:
** Download Lisptree in /tmp/lisptree/ and test it there. * (eepitch-shell) * (eepitch-kill) * (eepitch-shell) rm -Rfv /tmp/lisptree/ mkdir /tmp/lisptree/ git clone https://github.com/edrx/lisptree /tmp/lisptree/ maxima --no-init load("/tmp/lisptree/lisptree.mac"); lisptree(a[b,c][d,e](f,g)(h,i)); lisptree(fundef(format)); lisptree0_config('lisp)$ lisptree(fundef(format)); |
Here's the log of running that test block:
11. Maxima by Example
Update: See my page on (My)Qdraw.
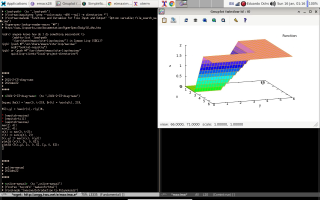
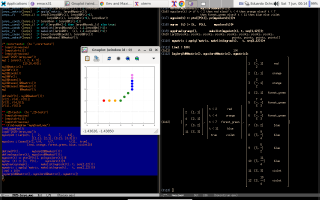
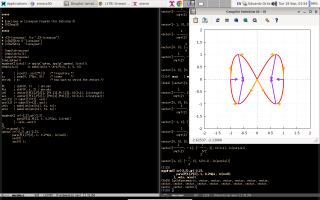
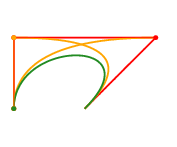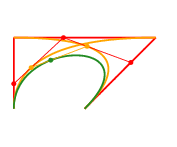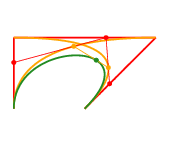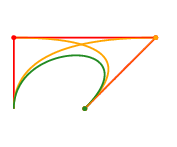
The best place for learning Maxima from examples is a (free) book whose name is - ta-daaa! - Maxima by Example. It is divided into chapters, and my script to download a local copy of it is here. Its chapter 13 is about qdraw, that is a front-end to Maxima's plot and draw commands. I find qdraw much easier to use than plot and draw; for example, the code for drawing the Lissajous figure below - with velocity and acceleration vectors! - is just this.
The second screenshot shows a trajectory P(t) = (cos t, sin t), the parabola Q(t) = P(0) + t·P'(0) + t2/2·P''(0), and my favorite trick - the boxes - for drawing parabolas by hand. Its code is here.
12. Qdraw and myqdraw
Update: See my page on (My)Qdraw.
Qdraw is easy to extend. I generated the animation below
with these files:
(find-angg "MAXIMA/myqdraw3.mac") (find-angg "MAXIMA/topdf1.mac") (find-angg "MAXIMA/mkanim1.sh") (find-angg "MAXIMA/bezier2.mac") |
Click on the animation to enlarge it; click here to see it in flipbook format.
12.1. Set comprehensions
Myqdraw contains a few DSLs (a.k.a. "little languages") - for example, this one for set comprehensions:
13. `displa_delegate'
One thing that I like a lot about Maxima is that it lets me use improvised notations - for example, I can draw something that looks similar enough to this
. | t=3 sin(t) | | t=4
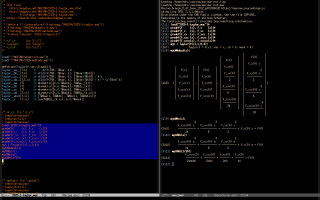
using matrices. The functions that I use to do the translation "in the right way" are in 2025-displa-delegate-2.lisp - see the screenshots below:
By "in the right way" I mean "in a way that lets me configure independently how _At2 objects are displayed in `display2d' style and in `tex1' style" - see the third and the fourth screenshots above.
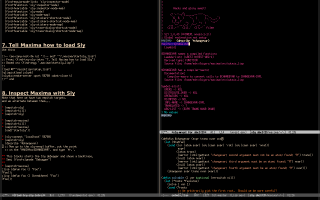
14. Debugging the Lisp (with Sly)
Update: in dec/2025 I found a way to make Slime work well with eepitch, and I recorded a video called "Badly-behaved targets" that explains that and a lot more. The rest of this section was written when I only knew how to use Sly.
Most people use Slime and Swank to debug the Lisp code of Maxima. I couldn't make Slime work with eepitch, so instead of Slime and Swank I'm using Sly, Slynk, and an eepitch-sly defined in this way, and I had to adapt these instructions. My code to use Sly and Slynk in Maxima is here: ~/.maxima/startsly.lisp.
My tutorial for making Sly work with Maxima is here: (find-try-sly-intro). Its last section -
(find-try-sly-intro "8. Inspect Maxima with Sly") |
shows - very briefly at the moment 🙁 - how we can use Sly to navigate Maxima's source files with `M-.', and how to get backtraces; in a backtrace we can inspect each stack frame, inspect the frame's local variables with the inspector, and even eval expressions in that frame.
See also these pages: 2025-calling-lua-from-common-lisp.html, eev-sly.html.