Dednat6: an extensible (semi-)preprocessor for LuaLaTeX that understands diagrams in ASCII art
The best introduction to Dednat6 is this presentation - and, in particular, its slides 7, 9, and 10. If you can't open PDFs click on the numbers to see them converted to PNGs; the PDF is here.
Let me start with a very short introduction.
(Lua)(La)TeX treats lines
starting with "%" as comments, and ignores them. This means that
we can put anything we want in these "%" lines - even code to be
processed by other programs besides *TeX. Dednat6 is a Lua program
that treats blocks of comments in a .tex file starting with "%D"
as specifications for diagrams, and blocks of comments starting with
"%:" as specifications for derivation trees.
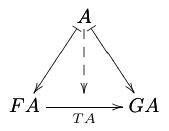
Here is an example of a .tex file with a block of "%D" lines:
\documentclass{article}
\usepackage{proof}
\input diagxy
\xyoption{curve}
\begin{document}
\catcode`\^^J=10
\directlua{dofile "dednat6load.lua"}
%D diagram T:F->G
%D 2Dx 100 +20 +20
%D 2D 100 A
%D 2D /|\
%D 2D v v v
%D 2D +30 FA --> GA
%D 2D
%D (( A FA |-> A GA |->
%D FA GA -> .plabel= b TA
%D A FA GA midpoint -->
%D ))
%D enddiagram
%D
$$\pu
\diag{T:F->G}
$$
\end{document}
|
If we compile that file with lualatex - a version of TeX that
can run Lua programs from inside TeX - we get a page with this
diagram:
I wrote the ancestors of dednat6 zillions of years
ago, to help me typeset categorical diagrams and Natural Deduction
trees for my mathematical research, but until 2018
these dednats were very very very hard to use if you weren't me. In
2018 I gave a presentation about dednat6 at TUG2018 (slides), published an article at
TUGBoat about it, and simplified Dednat6's initialization code a lot;
in 2019 I (finally) wrote decent minimal test files, created simple
ways to use dednat6 at sites that don't support lualatex like
Arxiv and EasyChair, cleaned up the package and this web page, and
wrote the quick start guide below.
Some links: The slides of my talk about Dednat6 at TUG2018. The big diagram from slide 7. My article about dednat6 at TUGBoat 39:3. A minimal test: demo-minimal.tex (HTML) (PDF) Other tests: demo-write-dnt.tex (HTML) (PDF) demo-write-single.tex (HTML) (PDF) demo-preproc.tex (HTML) (PDF) A Quick start guide. Zip file: http://anggtwu.net/dednat6.zip Git repository: https://github.com/edrx/dednat6 |
- 1. A quick start guide for beginners
- 2. The git repository
- 3.
dednat6.zip - 4. Hacking
- 5. Other back-ends: Tikz
- 6. The essential files
- 7. Main idea: heads
- 8. A big example
- 9. Emacs support
- 10. Dednat4 vs. Dednat6
- 11. When you can't use LuaLaTeX
- 12. "
\pu": process all dednat code until the current line - 13. "
output(...)" - 14. Special characters
- 15. LuaTeX
1. A quick start guide for beginners
If you use Overleaf:
- Download dednat6-minimal.zip
- Import the .zip
- Change the compiler to lualatex
- Click on "Recompile". You should get a PDF like this.
- Take a look at these slides and at the TUGBoat article
- Make small changes to demo-minimal.tex, recompile, rinse, repeat
If you use TeXstudio, TeXworks or something similar, then:
- Download and unpack dednat6.zip
- Edit demo-minimal.tex
- Set your editor font to some monospaced font
- Set your compiler to lualatex
- Compile demo-minimal.tex and view the PDF
- Make small changes to the deduction tree in ascii art, recompile, view
- Read the TUGBoat article.
Workaround for a bug: old versions of Dednat6 don't work on TeXLive/MikTeX/whateverTeX 2020, but updating Dednat6 should work. One person needed this temporary fix, but I believe that it is not needed anymore. If you have any problems please get in touch!
2. The git repository
Since 2019may21 dednat6 has a git repository.
If you're in a *NIX-based system you can
download dednat6 from there and test it with:
rm -Rfv /tmp/dednat6/ cd /tmp/ git clone https://github.com/edrx/dednat6 cd /tmp/dednat6/ make make clean |
The "make" will compile all its .tex files into PDFs; the "make clean" will delete all the generated files except the PDFs. After doing "make" and "make clean" open the file demo-minimal.tex, read its instructions and try to modify it and recompile it.
The git repository has most files from http://anggtwu.net/dednat6/, but not all - it doesn't include the PDFs and the HTMLs. Use the table below to access the HTMLized versions of the source files - in which most elisp hyperlinks become HTML hyperlinks - and the PDFs produced from the .tex files.
3. dednat6.zip
Most people will find it easier to work with the .zip package of dednat6 than with the git repository. The .zip contains all the files in the git archive plus the PDFs. Its URL is:
http://anggtwu.net/dednat6.zip |
The beginner-ish way to use it is to unpack it, read demo-minimal.tex and start modifying it - as in the quick start guide. If you are on a *NIX-like system and want to test it in the same way as we did with the git repository in the previous sections, the commands are:
rm -Rfv /tmp/dednat6/ mkdir /tmp/dednat6/ cd /tmp/dednat6/ wget http://anggtwu.net/dednat6.zip unzip dednat6.zip make veryclean make make clean |
The "make veryclean" is like "make clean" but it also
deletes the PDFs. "make" remakes the PDFs, but leaves some
intermediate files; "make clean" deletes these intermediate files
but leaves the PDFs... so the sequence of three "make"s above is
a way to check that are the PDF can be re-generated without errors.
4. Hacking
If you want to understand the innards of Dednat6 there are two recommended ways. First: most of the functions and data structures of Dednat6 are documented using "test blocks", and in 24jan2021 I make a short video explaing this. The page about that video has lots of links to documentation, and instructions to run the test blocks. Second: in 2020jun06 I wrote this:
dednat6/minimalcore.lua (HTML) demo-core.tex (HTML) (PDF) |
You can test it with:
rm -Rfv /tmp/dednat6core/ mkdir /tmp/dednat6core/ cd /tmp/dednat6core/ wget http://anggtwu.net/dednat6/demo-core.tex mkdir dednat6/ cd dednat6/ wget http://anggtwu.net/dednat6/dednat6/minimalcore.lua cd .. lualatex demo-core.tex |
In 2020apr18 made a (very, very, VERY bad) video about
hacking dednat6 and explaining some of my private extensions to it.
It's 72 minutes long. It's not at youtube or vimeo yet, but you can
access it as a 165MB .mp4 file here. It is based
on these executable notes:
http://anggtwu.net/dednat6/extra-modules.txt.html |
Long story short: if you know a bit of Emacs and eev then you can use the "test blocks" embedded in the source files of dednat6 to inspect the data structures... see:
(find-eev-quick-intro "6. Controlling shell-like programs") (find-eepitch-intro "3. Test blocks") (find-dednat6 "dednat6/diagtex.lua" "arrow_to_TeX-test") (find-dednat6 "dednat6/diagtex.lua" "arrows-tests") (find-dednat6 "dednat6/zhas.lua" "ZHA-tests") |
The directory dednat6/ currently contains several modules that are I wrote as quick hacks to typeset diagrams that I needed, and that I don't think that will be interesting to other people - except as curiosities, to show how extensible Dednat6 is. My paper Planar Heyting Algebras for Children (PDF, source tgz) uses many of these extensions; its draft sequel about closure operators (PDF, source tgz) uses a few more.
5. Other back-ends: Tikz
In feb/2020 I finally wrote a first alternative back-end for 2D diagrams - one that generates code for Tikz instead of code for diagxy. It is here:
demo-tikz.tex (HTML) (PDF) dednat6/diagtikz.lua (HTML) |
In nov/2020 Nathanael Arkor released Quiver (git repo here), and it looks great. I will try to make the TikZ back end of Dednat6 output code compatible with quiver.sty, but I won't have time to work on that before jan/2021.
6. The essential files
The demo below shows a way to compile demo-minimal.tex by unpacking only the
"essential files" from the .zip file - namely, demo-minimal.tex
itself, dednat6load.lua, and all the
.lua files in the directory dednat6/.
rm -Rfv /tmp/dednat6.zip cd /tmp/ wget http://anggtwu.net/dednat6.zip rm -Rfv /tmp/dn6-test-min/ mkdir /tmp/dn6-test-min/ cd /tmp/dn6-test-min/ unzip ../dednat6.zip "dednat6/**" dednat6load.lua demo-minimal.tex ls -l lualatex demo-minimal.tex ls -l |
7. Main idea: heads
(Lua)(La)TeX treats lines starting with "%" as comments, and
ignores them. This means that we can put anything we want in these
"%" lines - even code to be processed by other programs besides
*TeX.
Dednat6 read TeX files and pay attention only to the lines that
begin with some special sequences of characters (called "heads"), all
starting with "%". The main heads are:
| Head | interpreted as |
|---|---|
%L |
Lua code |
%: |
derivation trees (two-dimensional) |
%D |
definitions of diagrams (in a stack language) |
Dednat4 processes a TeX file, say, foo-4.tex, and produces an auxiliary TeX file, foo-4.dnt, containing the TeX code to typeset the derivation trees and diagrams of foo.tex. Dednat6 does something similar, but the TeX code is usually not saved to a file; instead, it is processed by TeX immediately. Let's look at two examples (in Dednat6 syntax):
%D diagram T:F->G
%D 2Dx 100 +20 +20
%D 2D 100 A
%D 2D / - \
%D 2D / | \
%D 2D v v v
%D 2D +25 FA ------> GA
%D 2D TA
%D (( A FA -> A GA ->
%D FA GA -> .plabel= b TA
%D A FA GA midpoint |->
%D ))
%D enddiagram
$$\pu
\diag{T:F->G}
$$
|
$$\defdiag{T:F->G}{
\morphism(300,0)/->/%
<-300,-375>[{A}`{FA};{}]
\morphism(300,0)/->/%
<300,-375>[{A}`{GA};{}]
\morphism(0,-375)|b|/->/%
<600,0>[{FA}`{GA};{TA}]
\morphism(300,0)/|->/%
<0,-375>[{A}`{\phantom{O}};{}]
}
\diag{T:F->G}
$$
|
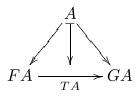
%: P\&Q
%: ----
%: P\&Q Q
%: ---- :f
%: P\&Q P R
%: :(P\&)f -------
%: P\&R P\&R
%:
%: ^t1 ^t2
%:
$$\pu
\ded{t1} := \ded{t2}
$$
|
$$\defded{t1}{
\infer*[{(P\&)f}]{ \mathstrut P\&R }{
\mathstrut P\&Q } }
\defded{t2}{
\infer[{}]{ \mathstrut P\&R }{
\infer[{}]{ \mathstrut P }{
\mathstrut P\&Q } &
\infer*[{f}]{ \mathstrut R }{
\infer[{}]{ \mathstrut Q }{
\mathstrut P\&Q } } } }
\ded{t1} := \ded{t2}
$$
|
8. A big example
Here is an example of a big diagram that I created with dednat6.
It appears at page 7 of my slides for TUG2018
(and in page 20 here).
(The source for the slides in included in dednat6.zip).
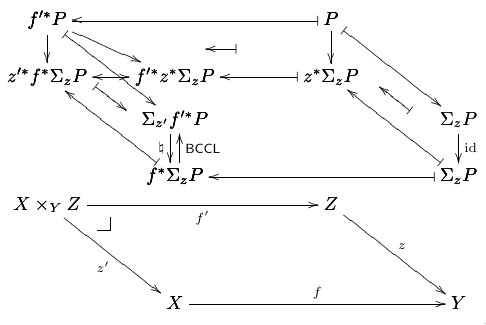
%D diagram BCCL-std
%D 2Dx 100 +45 +55 +45
%D 2D 100 B0 <====================== B1
%D 2D -\\ -\\
%D 2D | \\ | \\
%D 2D v \\ v \\
%D 2D +20 B2 <\\> B2' ============== B3 \\
%D 2D /\ \/ /\ \/
%D 2D +15 \\ B4 \\ B5
%D 2D \\ - \\ -
%D 2D \\ | \\|
%D 2D \\v \v
%D 2D +20 B6 <===================== B7
%D 2D
%D 2D +10 b0 |---------------------> b1
%D 2D |-> |->
%D 2D +35 b2 |--------------------> b3
%D 2D
%D ((
%D B0 .tex= f^{\prime*}P B1 .tex= P
%D B2 .tex= z^{\prime*}f^*Σ_zP B3 .tex= z^*Σ_zP
%D B4 .tex= Σ_{z'}f^{\prime*}P B5 .tex= Σ_zP
%D B6 .tex= f^*Σ_zP B7 .tex= Σ_zP
%D B2' .tex= f^{\prime*}z^*Σ_zP
%D B0 B1 <-| B0 B2 -> B0 B2' -> B1 B3 -> B2 B2' <-> B2' B3 <-|
%D B0 B4 |-> B1 B5 |->
%D B2 B6 <-| B3 B7 <-|
%D B6 B7 <-| B5 B7 -> .plabel= r \id
%D B4 B6 -> sl_ .plabel= l ♮ B4 B6 <- sl^ .plabel= r \BCCL
%D B0 B2' midpoint B1 B3 midpoint harrownodes nil 20 nil <-|
%D B0 B2 midpoint B4 B6 midpoint dharrownodes nil 20 nil |->
%D B1 B3 midpoint B5 B7 midpoint dharrownodes nil 20 nil <-|
%D ))
%D (( b0 .tex= X×_{Y}Z b1 .tex= Z b2 .tex= X b3 .tex= Y
%D b0 b1 -> .plabel= b f'
%D b0 b2 -> .plabel= l z'
%D b1 b3 -> .plabel= r z
%D b2 b3 -> .plabel= a f
%D b0 relplace 20 7 \pbsymbol{7}
%D ))
%D enddiagram
|
It uses some undocument hacks:
(find-dn6 "diagmiddle.lua" "harrownodes") (find-dn6 "diagmiddle.lua" "dharrownodes") (find-dn6 "diagforth.lua" "relplace") |
9. Emacs support
If you use Emacs you will probably want to load this:
dednat6.el (HTML) |
10. Dednat4 vs. Dednat6
Note: Dednat4 and Dednat6 are very similar. Dednat4 is easier to explain, because it is just a preprocessor that we have to run like this:
dednat4 foo-4.tex latex foo-4.tex |
Dednat6, in contrast, is easier to use - we just need this:
lualatex foo-6.tex |
In Dednat4 all the Lua code is run before running LaTeX; in
Dednat6, Lua is run from LuaLaTeX (with the command "\pu") to process chunks of foo-6.tex bit by bit. This is explained
in the TUGBoat
article, in section 3 ("semi-preprocessors"). To generate a .dnt file
with dednat6, see the next section.
11. When you can't use LuaLaTeX
Arxiv doesn't accept submissions that need LuaLaTeX to be compiled, and most journals also don't. Dednat6 currently implements three different ways to handle this. They are explained in these demos:
demo-write-dnt.tex (HTML) (PDF) demo-write-single.tex (HTML) (PDF) demo-preproc.tex (HTML) (PDF) |
If you need any help with this - or with anything else related to Dednat6 - please don't hesitate to get in touch! I need feedback, and excuses to write more docs...
...in particular, I use lots of UTF-8 characters in my .tex files, and in lualatex I can define them as this:
\catcode` =13 \def {\natural}
|
This doesn't work in TeX engines without Lua, like pdflatex. There are several possible workarounds, but the best ones, like newunicodechar, don't work in TeXLive 2016, that is what Arxiv uses. I've played with several different workarounds, and the one that looks the most solid uses lines like this
\DeclareUnicodeCharacter{266E}{\natural}
|
when Lua isn't available, instead of the "\catcode... \def..." thing above. I have not documented this properly yet.
12. "\pu": process all dednat code until the current line
The variable tf in dednat6 holds a TexFile object, and it is initialized by this code in LuaLaTeX:
\directlua{texfile(tex.jobname)}
|
If the current .tex file is foo-6.tex then tex.jobname is "foo-6", and this runs:
tf = TexFile.read("foo-6.tex")
|
which does, among other things,
tf.lines = splitlines(readfile "foo-6.tex") tf.nline = 1 |
If LuaLaTeX encounters at the line 23 of foo-6.tex the command
\pu, then it runs this, in Lua:
tf:processuntil(23) |
As tf.nline = 1, this means that Dednat6 has not processed any
dednat lines - the ones beginning with "%D", "%:", "%L", etc - yet; Dednat6 processes everything between lines 1 and 22,
and the result, which typically is some TeX code containg a series of
"\def"s, "\defdiag"s, and "\defded"s, is run at the
current point.
To understand this, take a look again at the table here
- the left column of the table contains high-level code with dednat
blocks, and the middle column contains the low-level code
corresponding to it, in which the "\pu"s have been replaced by
the "\defdiag"s and "\defded"s corresponding the diagrams
and trees defined in "%D" and "%:" lines using Dednat6
syntax.
If LuaLaTeX encounters the next \pu in foo-6.tex at line
54, then Dednat6 will process the dednat lines between lines 23 and 53
of foo-6.tex, and LaTeX will run the resulting "\def"s, "\defdiag"s, and "\defded"s.
13. "output(...)"
The functions from Dednat6 that produce LaTeX code - "\def"s,
"\defdiag"s, "\defded"s - use the function output(...),
defined here, to send that code to LaTeX
to make it be executed. In all the tests we have
this:
\directlua{verbose()}
|
it makes "output(...)" to be verbose, i.e., to always
print to the standard output the defs that will be sent to LaTeX.
The opposite of verbose() is:
\directlua{quiet()}
|
I am not sure if this verbose-mode output is sent also to the ".log" file; I think it should go there too.
14. Special characters
LuaLaTeX is UTF-8-based.
This means that we can use UTF-8 chars in our .tex files if we do
things like this,
\catcode`∀=13 \def∀{\forall}
\catcode`Θ=13 \defΘ{\Theta}
|
but some tricks, that I used a lot, do not work - they depended on all characters being 1-byte long and all codes between 0 and 255 being valid, including the ranges 1-7, 14-31, and 160-191.
The red stars ("*"s) in this document and in the page about dednat4 stand for "\^O"s; see this intro, especially the section
"Red stars" at the end.
I heard that LuaLaTeX on Windows rejects files with "*"s,
but I don't have the means for testing this myself or for finding
workarounds.
In dednat4, this was the standard way of adding "abbreviations" was this:
#:*->*\to * #:*|->*\mapsto * |
In dednat6 the best way to do something correspondent to that -
without using "*"s - is:
%L abbrevs:add("->", "\to ", "|->", "\\mapsto ")
|
In the tests for dednat6 I am trying to have some tests that use only ascii, some other ones that are latin-1, some that are "pure UTF-8", and a few tests that use the characters that may be causing problems with LuaLaTeX on Windows.
(...but at the moment very few test files are ready...)
15. LuaTeX
Dednat6 uses very little of LuaTeX at the moment - essentially just
tex.jobname, tex.inputlineno, tex.print from the Lua
side, and \directlua from TeX.
The following hacks were needed. 1) dednat6.lua loads this to make require behave like the require
from Lua. 2) Dednat6's output
function runs deletecomments to
filter out comments before sending code to tex.print. 3) I had to
use a
\catcode`\^^J=10 |
in the demos - 0.tex, 2.tex, 3.tex - to avoid having newlines become spurious "Ω"s.
My guess is that (2) and (3) are needed because tex.print and
\input use different catcode tables. At one point I tried to
check the details of this using this script
to run Rob Hoelz's lua-repl from
LuaLaTeX, but at some point I gave up.
One of the items in my to-do list is to make it easy to load and a Lua repl from dednat6. I sort of have an easy way now (2022), but I still need to document it properly... note that my first implementation of a repl in dednat6 - the one that appears in the screenshots in the pages 21 and 22 of the slides - used Rob Hoelz's lua-repl, then I dropped it and started using a minimalistic repl that I wrote myself, then I switched to the repl that I was also using in emlua, and now I switched to another minimalistic repl again - see my page on eev and TikZ for the details.
Recent questions (by me) on mailing lists:
2019-01-16:
Inspecting TeX tokens from a Lua REPL
2019-01-19:
Doubts about syntax: can <cs> and <pos> expand to <empty>?