Eduardo Ochs - Academic Research - Categorical Semantics, Downcasing Types, Skeletons of Proofs, and a bit of Non-Standard Analysis
The best things here are marked like [this].
Quick index:- Lógica pra pessoas que sabem resolver 2+x=5 mas... (2026)
- Adapting Lean tutorials to the Brazilian case (2025)
- Panic! At Equalities (Versão Teresópolis) (2024)
- On a way to visualize some Grothendieck Topologies (2022)
- On the missing diagrams in Category Theory (2022) ******
- Grothendieck Topologies for Children (2021)
- Category Theory as An Excuse to Learn Type Theory (2021) **
- Each closure operator induces a topology and vice-versa (2020/2021) ***
- On my favorite conventions for drawing the missing diagrams in Category Theory (2020) ***
- Notes on Notation (2020)
- What kinds of knowledge do we gain by doing CT in several levels of abstraction in parallel? (2020)
- Notes about classifiers and local operators in a Set^(P,A) (2020)
- On two tricks to make Category Theory fit in less mental space (2019)
- Using Planar Heyting Algebras to develop visual intuition about IPL (2019)
- On some missing diagrams in the Elephant (2019) *
- Notes on the Yoneda Lemma (2019/2020)
- An introduction to type systems (and to the "Logic for Children" project) (2019)
- Five applications of the "Logic for Children" project to Category Theory (2019)
- Ensinando Matemática Discreta para calouros com português muito ruim (2019)
- How to almost teach Intuitionistic Logic to Discrete Mathematics Students (2019) *
- Dednat6: an extensible (semi-)preprocessor for LuaLaTeX *
- Logic for Children (workshop at UniLog 2018) *
- Visualizing Geometric Morphisms (talk at UniLog 2018)
- Planar Heyting Algebras for Children (2017-) ***
- Notes on notation (2017)
- IPL For Children and Meta-Children, or: How Archetypal Are ZHAs? (2017)
- Lambda-calculus, logics and translations (course, 2016-)
- Intuitionistic Logic for Children, or: Planar Heyting Algebras for Children (2015)
- Logic and Categories, or: Heyting Algebras for Children (2015)
- Sheaves for children (2014)
- Sheaves on Finite DAGs may be Archetypal (2011)
- Internal Diagrams in Category Theory (2010/2013) ***
- Downcasing Types (at UniLog'2010)
- Natural infinitesimals in filter-powers (2008)
- Sheaves for Non-Categorists (2008)
- Seminar on downcasing types (nov/2007)
- General links
- PhD and post-PhD research *
- MsC Thesis and related things *
- Typesetting categorical diagrams in LaTeX
Note: I use Dednat6 to draw most of my diagrams.
The LaTeX source of my PDFs is always available - or should be.
To download the LaTeX source of a PDF calledfoo.pdftry:
wget http://anggtwu.net/LATEX/foo.tgz
wget http://anggtwu.net/LATEX/foo.zip
then unpack it and runlualatex foo.tex.
If neither the.tgznot the.zipare online, get in touch!
Lógica pra pessoas que sabem resolver 2+x=5 mas... (2026)
 My presentation at the World Logic Day 2026, in 2026jan14. This was my first "serious"
presentation about Mathematical Education; it was in Portuguese and
with most slides in Portuguese, but most of the items of the
bibliography were in English. The translation of its title to English
is "Logic for people who know how to solve 2+x=5 but who don't
know how to substituir x by 3 in 2+x=5"; the "people" in the title
are many of the students that are taking Calculus 2 in the campus in
which I work.
My presentation at the World Logic Day 2026, in 2026jan14. This was my first "serious"
presentation about Mathematical Education; it was in Portuguese and
with most slides in Portuguese, but most of the items of the
bibliography were in English. The translation of its title to English
is "Logic for people who know how to solve 2+x=5 but who don't
know how to substituir x by 3 in 2+x=5"; the "people" in the title
are many of the students that are taking Calculus 2 in the campus in
which I work.
The full title in Portuguese is:
Lógica pra pessoas que sabem resolver 2+x=5 mas não sabem substituir x por 3 em 2+x=5
Slides.
Video (version with my presention only).
Lógica Ladeira Abaixo
- the channel of the organizers.
They said that they will release the video with all presentations soon.
Adapting Lean tutorials to the Brazilian case (2025)
My presentation at the EBL 2025 (in 2025may13).
Slides (unrevised).
Panic! At Equalities (Versão Teresópolis) (2024)
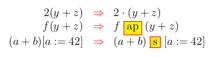 This was my presentation at the "Retiro de Teresópolis" in
2024jun18. The "Retiro" doesn't have a page yet, but it was
organized by the same people who organized these meetings. My presentation was in
Portuguese and with slides in Portuguese, and it was mainly about
the techniques that I've been using to teach Calculus 2 (page, PDFzão) to the
students of Rio das Ostras, that usually arrive at the course
without knowing how to manipulate expressions.
This was my presentation at the "Retiro de Teresópolis" in
2024jun18. The "Retiro" doesn't have a page yet, but it was
organized by the same people who organized these meetings. My presentation was in
Portuguese and with slides in Portuguese, and it was mainly about
the techniques that I've been using to teach Calculus 2 (page, PDFzão) to the
students of Rio das Ostras, that usually arrive at the course
without knowing how to manipulate expressions.
On a way to visualize some Grothendieck Topologies (2022)
My presentation at the XX EBL (sep/2022).
Slides,
LaTeX source,
abstract.
See my "Grothendieck Topologies for Children" (2021).
On the missing diagrams in Category Theory (2022) ******
[MD] This is a rewrite of [FavC]. Its abstract is:
 Most texts on Category Theory are written in a very terse style, in
which people pretend a) that all concepts are visualizable, and b)
that the readers can reconstruct the diagrams that the authors had
in mind based on only the most essential cues. As an outsider I
spent years believing that the techniques for drawing diagrams were
part of the oral culture of the field, and that the insiders could
read texts on CT reconstructing the "missing diagrams" in them line
by line and paragraph by paragraph, and drawing for each page of
text a page of diagrams with all the diagrams that the authors had
omitted. My belief was wrong: there are lots of conventions for
drawing diagrams scattered through the literature, but that unified
diagrammatic language did not exist. In this chapter I will show an
attempt to reconstruct that (imaginary) language for missing
diagrams: we will see an extensible diagrammatic language, called
DL, that follows the conventions of the diagrams in the literature
of CT whenever possible and that seems to be adequate for drawing
"missing diagrams" for Category Theory. Our examples include the
"missing diagrams" for adjunctions, for the Yoneda Lemma, for Kan
extensions, and for geometric morphisms, and how to formalize them
in Agda.
Most texts on Category Theory are written in a very terse style, in
which people pretend a) that all concepts are visualizable, and b)
that the readers can reconstruct the diagrams that the authors had
in mind based on only the most essential cues. As an outsider I
spent years believing that the techniques for drawing diagrams were
part of the oral culture of the field, and that the insiders could
read texts on CT reconstructing the "missing diagrams" in them line
by line and paragraph by paragraph, and drawing for each page of
text a page of diagrams with all the diagrams that the authors had
omitted. My belief was wrong: there are lots of conventions for
drawing diagrams scattered through the literature, but that unified
diagrammatic language did not exist. In this chapter I will show an
attempt to reconstruct that (imaginary) language for missing
diagrams: we will see an extensible diagrammatic language, called
DL, that follows the conventions of the diagrams in the literature
of CT whenever possible and that seems to be adequate for drawing
"missing diagrams" for Category Theory. Our examples include the
"missing diagrams" for adjunctions, for the Yoneda Lemma, for Kan
extensions, and for geometric morphisms, and how to formalize them
in Agda.
This was published as a
chapter
of this book:
Handbook of Abductive Cognition.
The current ("first-person") version is here.
The version on Arxiv (also "first-person") is here:
PDF,
abstract.
The technical report "On the missing diagrams in Category
Theory: Agda code" will be at this
link.
The version accepted into the "Handbook of Abductive Cognition" is drier and shorter: it is not in the first person, it has a much shorter introduction, and it doesn't have the chapter that shows extensions of the diagrammatic language. I think that the first-person version is much better. =/
Grothendieck Topologies for Children (2021)
 The paper "Planar Heyting Algebras for Children" (here) showed how to use Planar Heyting
Algebras to visualize the truth-values and the operations of
Propositional Calculus in certain toposes; the "...for children" of
its title means: "we will start from some motivating examples ('for
children') that are easy to visualize, and then go the general case
('for adults') - but there are precise techniques for working
on the case 'for children' and on the case 'for adults' in
parallel". These techniques are described in detail here.
In these notes we will use these techniques to visualize
Grothendieck topologies - first in the "archetypal" case of the
canonical topology on a certain finite topological space, and then
we will generalize that to arbitrary Grothendieck topogies on
certain finite posets. that we will treat as "ex-topologies".
The paper "Planar Heyting Algebras for Children" (here) showed how to use Planar Heyting
Algebras to visualize the truth-values and the operations of
Propositional Calculus in certain toposes; the "...for children" of
its title means: "we will start from some motivating examples ('for
children') that are easy to visualize, and then go the general case
('for adults') - but there are precise techniques for working
on the case 'for children' and on the case 'for adults' in
parallel". These techniques are described in detail here.
In these notes we will use these techniques to visualize
Grothendieck topologies - first in the "archetypal" case of the
canonical topology on a certain finite topological space, and then
we will generalize that to arbitrary Grothendieck topogies on
certain finite posets. that we will treat as "ex-topologies".
The PDF is here, but it is a mess. I rewrote most of the important ideas cleanly here.
I give two informal talks on that, both in Portuguese, here.
The first one was in may 17, 2021, and was a bit messy. Recording.
The second one was in june 7, 2021, and was much better. Youtube, better quality recording.
slides.
Category Theory as An Excuse to Learn Type Theory (2021) **
 The organizers of the "Encontro Brasileiro em Teoria das Categorias" invited me to give a
50-minute talk there. My talk was on the thursday, 28
january 2021. The abstract for my talk is here, and the slides
are here. The
recording is here (in Portuguese).
The organizers of the "Encontro Brasileiro em Teoria das Categorias" invited me to give a
50-minute talk there. My talk was on the thursday, 28
january 2021. The abstract for my talk is here, and the slides
are here. The
recording is here (in Portuguese).
Each closure operator induces a topology and vice-versa (2020/2021) ***
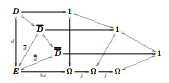 [Clops&Tops]
One of the main prerequisites for understanding sheaves on
elementary toposes is the proof that a (Lawvere-Tierney) topology
on a topos induces a closure operator on it, and vice-versa. That
standard theorem is usually presented in a relatively brief way,
with most details being left to the reader, and with no hints on
how to visualize some of the hardest axioms and proofs.
[Clops&Tops]
One of the main prerequisites for understanding sheaves on
elementary toposes is the proof that a (Lawvere-Tierney) topology
on a topos induces a closure operator on it, and vice-versa. That
standard theorem is usually presented in a relatively brief way,
with most details being left to the reader, and with no hints on
how to visualize some of the hardest axioms and proofs.
These notes are, on a first level, an attempt to present that standard theorem in all details and in a visual way, following the conventions below; in particular, some properties, like stability by pullbacks, are always drawn in the same "shape".
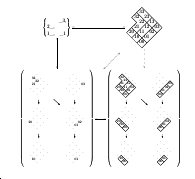 On a second level these notes are also an experiment on doing these
proofs on "archetypal cases" in ways that makes all the proofs easy
to lift to the "general case". Our first archetypal case is a
"topos with inclusions". This is a variant of the "toposes with
canonical subobjects" from section 2.15 of [Lambek/Scott 86];
all toposes of the form Set^C, where C is a small category, are
toposes with inclusions, and when we work with toposes with
inclusions concepts like subsets and intersections are very easy to
formalize. We do all our proofs on the correspondence between
closure operators and topologies in toposes with inclusions, and
then we show how to lift all our proofs to proofs that work on any
topos. Our second archetypal case is toposes of the form Set^D,
where D is a finite two-column graph. We show a way to visualize
all the Lawvere-Tierney topologies on toposes of the form Set^D,
and we define formally a way to "add visual intuition to a proof
about toposes"; this is related to the several techniques for doing
"Category Theory for children" that are explained in the first
sections of [FavC].
On a second level these notes are also an experiment on doing these
proofs on "archetypal cases" in ways that makes all the proofs easy
to lift to the "general case". Our first archetypal case is a
"topos with inclusions". This is a variant of the "toposes with
canonical subobjects" from section 2.15 of [Lambek/Scott 86];
all toposes of the form Set^C, where C is a small category, are
toposes with inclusions, and when we work with toposes with
inclusions concepts like subsets and intersections are very easy to
formalize. We do all our proofs on the correspondence between
closure operators and topologies in toposes with inclusions, and
then we show how to lift all our proofs to proofs that work on any
topos. Our second archetypal case is toposes of the form Set^D,
where D is a finite two-column graph. We show a way to visualize
all the Lawvere-Tierney topologies on toposes of the form Set^D,
and we define formally a way to "add visual intuition to a proof
about toposes"; this is related to the several techniques for doing
"Category Theory for children" that are explained in the first
sections of [FavC].
The PDF of the
current version (2021jul26). Arxiv.
Older versions: 2020nov24.
See also: "On a formula
that is not in Grothendieck Topologies in Posets'" (Arxiv).
On my favorite conventions for drawing the missing diagrams in Category Theory (2020) ***
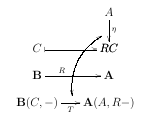 [FavC]
I used to believe that my conventions for drawing diagrams for
categorical statements could be written down in one page or less,
and that the only tricky part was the technique for reconstructing
objects "from their names"... but then I found out that this is not
so.
[FavC]
I used to believe that my conventions for drawing diagrams for
categorical statements could be written down in one page or less,
and that the only tricky part was the technique for reconstructing
objects "from their names"... but then I found out that this is not
so.
This is an attempt to explain, with motivations and examples, all the conventions behind a certain diagram, called the "Basic Example" in the text. Once the conventions are understood that diagram becomes a "skeleton" for a certain lemma related to the Yoneda Lemma, in the sense that both the statement and the proof of that lemma can be reconstructed from the diagram. The last sections discuss some simple ways to extend the conventions; we see how to express in diagrams the ("real") Yoneda Lemma and a corollary of it, how to define comma categories, and how to formalize the diagram for "geometric morphism for children" mentioned in section 1.
People in CT usually only share their ways of visualizing things when their diagrams cross some threshold of of mathematical relevance - and this usually happens when they prove new theorems with their diagrams, or when they can show that their diagrams can translate calculations that used to be huge into things that are much easier to visualize. The diagrammatic language that I present here lies below that threshold - and so it is a "private" diagrammatic language, that I am making public as an attempt to establish a dialogue with other people who have also created their own private diagrammatic languages.
PDF, arxiv.
The non-arxiv PDF is better - it has colors and hyperlinks.
See [MD] for a rewritten version of these notes.
Notes on Notation (2020)
In 2020 I decided to test my conventions
for drawing missing diagrams by drawing
some of the diagrams that are "missing" in several texts and seeing if
I always get diagrams that are easy to translate into Idris. These are
messy notes for personal use, but if you have your own conventions I'd
love to see them - please get in touch.
More "*"s mean more interesting.
Abramsky/Tzevelekos,
Awodey's book,
Badiou's "Logics of Worlds",
Badiou's "Mathematics of The Transcendental",
Barr/Wells's CTCS,
Bell's "Toposes and Local Set Theories",
Diaconescu's "Institutions...", *
Jacobs's "Categorical Logic and Type Theory", **
Kock's "A Simple Axiomatics for Differentiation",
Lambek86,
Lawvere's "Adjointness in Foundations" (1969),
Lawvere's "Equality in Hyperdoctrines" (1970),
MacDonald/Sobral,
MacLane's CWM,
MacLane/Moerdijk's "Sheaves in Geometry and Logic", *
McLarty's "Elementary Categories, Elementary Toposes", *
Reyes*2/Zolfaghari's "Generic Figures...",
Riehl's "Categories in Context",
Seely's "Hyperdoctrines...", **
Seely's "LCCCs and Type Theory",
Valeria de Paiva's "The Dialectica Categories"
What kinds of knowledge do we gain by doing CT in several levels of abstraction in parallel? (2020)
A talk that I submitted to Diagram 2020. Its short abstract is:
Concepts and proofs in Category Theory are usually presented in a very abstract way, in which the diagrams, the motivating examples and the low-level details are mostly omitted and left as exercises for the reader. Here we will discuss how to work in this more abstract level and in less abstract levels at the same time, using parallel diagrams and transfering some information from the more abstract diagram to the less abstract one and back - and we will show formally, using type systems, what we gain by working in two levels of abstraction in parallel.
Its "real", 4-page abstract is here.
Notes about classifiers and local operators in a Set^(P,A) (2020)
In the last section of Planar Heyting
Algebras for Children 2: Local Operators, J-Operators, and
Slashings (PDF)
I wrote that the proofs that my definitions for Ω and j "work as expected" are "routine". Well, they are only routine
if you know some techniques... these notes will
discuss these techniques and show all the calculations, but they
are currently in a very preliminary form.
The PDF.
On two tricks to make Category Theory fit in less mental space (2019)
A talk at the Creativity
2019 in Rio de Janeiro, in the workshop on formal logic and foundations.
Its full title was "On two tricks to make Category Theory fit in
less mental space: missing diagrams and skeletons of proofs", and
the abstract that I submitted is here.
[LessMS]
Slides.
Using Planar Heyting Algebras to develop visual intuition about IPL (2019)
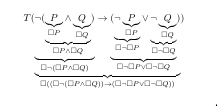 Two presentations with the same title in two small events.
Two presentations with the same title in two small events.
The first one was in 2019aug19 at the "Jornadas de Mirantão"
at Ilha Grande, and in it I alternated between its slides and
my slides for the
World Logic Day 2019.
The second one was in 2019sep10 at the "Seminário do Hermann" at PUC-Rio, and
in it I alternated between its slides and
the Planar
Heyting Algebras for Children paper (see here).
I did not prepare abstracts for them.
On some missing diagrams in the Elephant (2019) *
 [MDE] This is a 12-page extended abstract
(also here
with darker fonts) that I submitted to ACT2019, that happened in Oxford
in july 2019. The extended abstract's abstract is:
[MDE] This is a 12-page extended abstract
(also here
with darker fonts) that I submitted to ACT2019, that happened in Oxford
in july 2019. The extended abstract's abstract is:
Imagine two category theorists, Aleks and Bob, who both think very visually and who have exactly the same background. One day Aleks discovers a theorem, T1, and sends an e-mail, E1, to Bob, stating and proving T1 in a purely algebraic way; then Bob is able to reconstruct by himself Aleks's diagrams for T1 exactly as Aleks has thought them. We say that Bob has reconstructed the "missing diagrams" in Aleks's e-mail.
Now suppose that Carol has published a paper, P2, with a theorem T2. Aleks and Bob both read her paper independently, and both pretend that she thinks diagrammatically in the same way as them. They both "reconstruct the missing diagrams" in P2 in the same way, even though Carol has never used those diagrams herself.
Here we will reconstruct, in the sense above, some of the "missing diagrams" in two factorizations of geometric morphisms in section A4 of Johnstone's "Sketches of an Elephant", and also some "missing examples". Our criteria for determining what is "missing" and how to fill out the holes are essentially the ones presented in the "Logic for Children" workshop at the UniLog 2018; they are derived from a certain definition of "children" that turned out to be especially fruitful.
My submission was not accepted to become a talk, only to the poster session (on tuesday 16/july).
The PDF of
the poster. I wrote INCOMPLETE at the bottom
of it by hand when I hanged it to the wall.
The poster makes reference to these papers, notes, and slides:
- PH1 ("Planar Heyting Algebras for Children"): PDF, more info.
- PH2 ("Planar Heyting Algebras for Children 2: Local Operators"): PDF, more info.
- NYo ("Notes on the Yoneda Lemma"): PDF, more info.
- MDE ("On some missing diagrams in the Elephant"): PDF of the extended abstract.
- IDARCT ("Internal Diagrams and Archetypal Reasoning in Category Theory"): PDF, more info.
See the "Planar Heyting Algebras for Children" series.
Notes on the Yoneda Lemma (2019/2020)
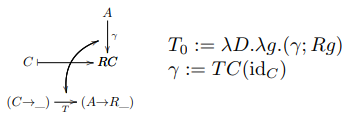 [NYo]
Slides,
My plan was to make a video from this, but I got stuck...
[NYo]
Slides,
My plan was to make a video from this, but I got stuck...
Then some friends asked me to present this to them in Portuguese
by Zoom in 2020may29, and they recorded it. Then I
got unstuck -
and I wrote the paper "On my favorite
conventions..."
and declared these slides obsolete.
The full title of the slides is:
A diagram for the Yoneda Lemma
(In which each node and arrow can be
interpreted precisely as a "term",
and most of the interpretations are
"obvious"; plus dictionaries!!!)
I am trying to implement this in a proof assistant -
on top of Jannis Limpberg's work or on idris-ct -
but I am progressing slowly! Help, please!!!
Here is my eev-ized version of the Idris tutorial.
Older versions of the slides:
2020-04-05,
2019-06-01.
If you don't know the Yoneda Lemma well
then start by these blog posts:
E,
L.
An introduction to type systems (and to the "Logic for Children" project) (2019)
 This is going to be a series of videos, but I am still
working on the slides... work in progress!
This is going to be a series of videos, but I am still
working on the slides... work in progress!
Preliminary mini-abstract: once we learn a bit of
type systems - the Barendregt Cube and BHK; the Calculus
of Constructions is not really needed - we can use the
techniques of the "Logic for Children" project to build diagrams
for categorical concepts in a way in which every node and arrow
in these diagrams can be interpreted precisely as a lambda term;
moreover, we can create "dictionaries" based on those diagrams
that help us translate between several standard notations found
in the literature - and help us read the standard literature.
Links to some of the slides (work in progress!):
1. [NTy] An
introduction to Type Theory (40% ready).
2. Notes on the
Yoneda Lemma (90% ready; moved to the item above)
I almost gave a presentation about the part on types at IFCS in 2019jun18, but Jean-Yves Beziau forgot to pick up the projector from the secretary's drawer in the morning... she left everything locked, went out for lunch and only returned many, many hours later.
Five applications of the "Logic for Children" project to Category Theory (2019)
A talk that I gave at the EBL2019 in 2019may09. Its abstract is here. My plans for this talk were very ambitious: I wanted to present the main ideas, motivations and constructions of PHAfC 1, 2 and 3 and Logic for Children in 20 minutes, with lots of figures... but when it was my turn to present all the people who knew a bit of Category Theory were in another room, attending a session with technical talks, and I did not have the 5 or 6 slides that I could have made my talk more accessible to an audience of philosophers. I failed miserably.
Slides.Ensinando Matemática Discreta para calouros com português muito ruim (2019)
I organized a round table about how to teach Logic
to undergraduates in the EBL2019.
Its abstracts are here
(in Portuguese). It happened in 2019may06.
The slides of my talk - about a way to teach Discrete Mathematics
to freshmen who speak and write Portuguese very badly - are here (about 70%
in English).
How to almost teach Intuitionistic Logic to Discrete Mathematics Students (2019) *
 A talk in the World Logic
Day - 2019jan14 - in Rio de
Janeiro, about:
A talk in the World Logic
Day - 2019jan14 - in Rio de
Janeiro, about:
1) my approach to teaching Discrete Mathematics to the students
that we get nowadays,
2) my course without prerequisites on lambda-calculus
and intuitionistic logic, and
3) how this fits at the base of the Logic for Children project.
Slides.
Dednat6: an extensible (semi-)preprocessor for LuaLaTeX *
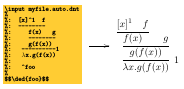 A talk at TUG2018, in Rio de
Janeiro, in 2018jul20 about
the package that I use to typeset several kinds of
diagrams.
A talk at TUG2018, in Rio de
Janeiro, in 2018jul20 about
the package that I use to typeset several kinds of
diagrams.
Its full title is "Dednat6: an extensible (semi-)preprocessor for
LuaLaTeX that understands diagrams in ASCII art".
2018-12-31: Official page: http://anggtwu.net/dednat6.html
2018-10-29: Revised version of the article about
Dednat6 to TUGboat. PDF, source; published in
TUGBoat
39:3.
2018-10-16: Original version of the article about Dednat6 to
TUGboat: PDF, source. Has some very ugly line breaks.
2018-07-20: First day of the Conference. Program, my slides and a video of my
presentation (without me jumping to point to things).
2018-05-08: Abstract submitted to the conference.
Logic for Children (workshop at UniLog 2018) *
 I organized (with Fernando Lucatelli) a workshop called "Logic for Children" that
happened at the UniLog 2018 in
Vichy, France, in june 24, 2018.
I organized (with Fernando Lucatelli) a workshop called "Logic for Children" that
happened at the UniLog 2018 in
Vichy, France, in june 24, 2018.
[LFCV] I made a video to advertise the workshop. It was based on these slides. I took
the pentomino image from here.
[LFC] Here is its
unofficial page, that has lots of links and
resources.
Here is the official page
of the workshop.
Here is its
original description and call for papers in PDF form.
Visualizing Geometric Morphisms (talk at UniLog 2018)
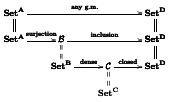 A talk given at the workshop "Categories and Logic" in the
UniLog 2018 in june 22, 2018.
A talk given at the workshop "Categories and Logic" in the
UniLog 2018 in june 22, 2018.
Its subtitle was "An application of the "Logic for Children" project to
Category Theory".
Abstract.
[VGM]
Slides.
Planar Heyting Algebras for Children (2017-) ***
 Finite planar Heyting Algebras ("ZHA"s) are very good tools for
teaching Heyting Algebras and Intuitionistic
Propositional Logic to "children"; "children" here means "people
without mathematical maturity", in the sense that they are not able
to understand structures that are too abstract straight away, they
need particular cases first.
Finite planar Heyting Algebras ("ZHA"s) are very good tools for
teaching Heyting Algebras and Intuitionistic
Propositional Logic to "children"; "children" here means "people
without mathematical maturity", in the sense that they are not able
to understand structures that are too abstract straight away, they
need particular cases first.
This is going to be a series of three papers.
[PH1] The first paper, called "Planar Heyting Algebras for Children", is about intuitionistic logic and ZHAs, and about the relation between ZHAs and topological semantics. It has been tested on real "children" - sophomore CS students! - and it was published in the South American Journal of Logic, vol.5, no.1.
[PH2]
The second paper, called "Planar Heyting Algebras for Children 2: J-Operators, Slashings, and Nuclei", is about a way to visualize nuclei on ZHAs; nuclei are the basis for building sheaves. There is a version of it on arxiv, as arXiv:2001.08338, and the current version is here. I am rewriting some of its sections (for the n-th time).
[PH3] The third paper - with Peter Arndt, about tools for visualizing some of the material about geometric morphisms and sheaves in section A4 of Johnstone's Sketches of an Elephant - is still in gestation, but the extended abstract called "On some missing diagrams in the Elephant" (PDF) - that I submitted to the ACT2019 contains many of the ideas that will be on it.
Related:
"On my favorite conventions..." - a
broad view of the "for children" project, with concrete examples
(2020). Start by this!
"Visualizing geometric
morphisms" - my talk about the third paper at the
UniLog2018.
"Logic for Children"
- a workshop that I organized at the UniLog2018.
Page,
video,
slides.
When I present this to "real" children who don't know
lambda notation we go through this
material first.
Notes on notation (2017)
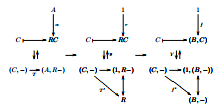 "Different people have different measures for "mental space";
someone with a good algebraic memory may feel that an expression like
[...] is easy to remember, while I always think diagramatically,
and so what I do is that I remember this diagram [...] and I
reconstruct the formula from it." (IDARCT)
"Different people have different measures for "mental space";
someone with a good algebraic memory may feel that an expression like
[...] is easy to remember, while I always think diagramatically,
and so what I do is that I remember this diagram [...] and I
reconstruct the formula from it." (IDARCT)
These are very informal notes showing my favourite ways to draw the "missing diagrams" in MacLane's CWM, and my favourite choice of letters for them. Work in progress changing often, contributions and chats welcome, etc. My plan is to do something similar for parts of the Elephant next.
A skeleton for the Yoneda Lemma (PDF).
Notes on notation: CWM (PDF).
Notes on notation: Elephant (PDF).
IPL For Children and Meta-Children, or: How Archetypal Are ZHAs? (2017)
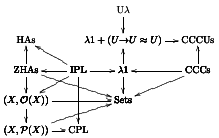 This is a 20-minute talk that I gave in the
EBL2017 in 2017may09.
This is a 20-minute talk that I gave in the
EBL2017 in 2017may09.
The full title is:
"Intuitionistic Propositional Logic For Children and Meta-Children,
or: How Archetypal Are Finite Planar Heyting Algebras?"
It is an introduction to the material in
Planar Heyting Algebras for Children.
Abstract: PDF.
Slides: PDF
Handouts: PDF.
Lambda-calculus, logics and translations (course, 2016-)
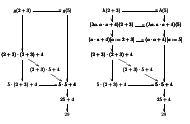 In 2016 I started giving a very introductory
course on lambda-calculus, types, intuitionistic propositional logic,
Curry-Howard, Categories, Lisp and Lua in the campus
where I work. The course is 2hs/week, has no prerequisites at all, has
no homework, and is usually attended by 2nd/3rd semester CompSci
students; they spend most of their time in class discussing and doing
exercises together in groups on a whiteboard.
In 2016 I started giving a very introductory
course on lambda-calculus, types, intuitionistic propositional logic,
Curry-Howard, Categories, Lisp and Lua in the campus
where I work. The course is 2hs/week, has no prerequisites at all, has
no homework, and is usually attended by 2nd/3rd semester CompSci
students; they spend most of their time in class discussing and doing
exercises together in groups on a whiteboard.
I have LaTeXed a part of the material; it's here. For bibliography, images of the whiteboards, etc, go here.
Intuitionistic Logic for Children, or: Planar Heyting Algebras for Children (2015)
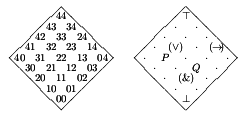 Seminar notes, with lots of figures (all drawn with Dednat6).
Seminar notes, with lots of figures (all drawn with Dednat6).
Not self-contained. Superseded by this.
I never wrote a textual abstract for this, but the page 2 of the
PDF is a nice "One
page intro" with text and diagrams.
The PDF is here
(and here).
Current version: 2015oct19b.
(First version: 2015sep24.)
Logic and Categories, or: Heyting Algebras for Children (2015)
 A tutorial presented at the UniLog 2015 conference (Istanbul), 20-22/jun/2015.
A tutorial presented at the UniLog 2015 conference (Istanbul), 20-22/jun/2015.
Abstract: PDF,
HTML.
Slides: PDF.
Handouts: PDF.
Notes on a meaning for "for children": PDF.
Sheaves for children (2014)
 A 20-minute talk - here are its slides - presented at the XIV EBL, on 2014apr09. Its abstract:
A 20-minute talk - here are its slides - presented at the XIV EBL, on 2014apr09. Its abstract:
First-year university students - the ``children'' of the title - often prefer to start from an interesting particular case, and only then proceed to general statements. How can we make intuitionistic logic, toposes, and sheaves accessible to them?
Let D be a finite subset of N2. Draw arrows for all the ``black pawns moves'' between points of D, and let D be the poset generated by that graph; D is what we call a ``ZDAG'', and SetD is a ``ZDAG-topos''. It turns out that the truth-values of a SetD can be represented in a very nice way as two-dimensional ASCII diagrams, and that all the operations leading to sheaves and geometric morphisms can be understood via algorithms on diagrams.
In this talk we will present a computer library for performing computations interactively on the truth-values of ZDAG-toposes. The diagrams are rendered in ASCII by default, but there is a module that typesets them in LaTeX.
The second - and much longer - version of this talk (at the Seminário Carioca de Lógica, 2014may19, 15:00, IFCS) had these slides and these handouts, and was meant for much younger "children". The focus this time was a visual characterization of the subsets of N2 that are Heyting Algebras, and how can we treat their points as truth-values, and so how to interpret intuitionistic logic on them. I call these subsets "ZHAs", the definitions and main theorems for them are in the pages 20 to 27 of the slides, and also at the handouts.
Sheaves on Finite DAGs may be Archetypal (2011)
 Can the ideas of my article about "internal
diagrams" be used to present the basic concepts of toposes and
sheaves starting from simple, "archetypal" examples? I believe so, but
this is still a work in progress!
Can the ideas of my article about "internal
diagrams" be used to present the basic concepts of toposes and
sheaves starting from simple, "archetypal" examples? I believe so, but
this is still a work in progress!
Here are 7 pages of very nice handwritten notes (titled "Sheaves for Children"): pdf, djvu. They were written after discussions with Hugo Luiz Mariano and Claus Akira Matsushige Horodynski in feb/2012, during a minicourse on CT in Brasilia organized by Claus, with me and Hugo as lecturers...
...and here are some slightly older notes - I submitted them, in a admittedly incomplete form, to the XVI EBL, with this abstract - and then I did a bad job at presenting them; here are the slides, they cover only the first ideas =(.
For the sake of completeness, here are some handwritten diagrams describing Kan extensions in an (hopefully) archetypal case, motivated by discussions with G.F. Lima: 1200dpi djvu, 600dpi djvu, 600dpi pdf.
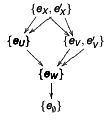
Internal Diagrams in Category Theory (2010/2013) ***
 [IDARCT]
A paper that I published at Logica Universalis in
its special
issue on Categorical Logic in 2013.
[IDARCT]
A paper that I published at Logica Universalis in
its special
issue on Categorical Logic in 2013.
The published version has some weirdly-sized figures and some ugly
page breaks. The preprint is much
better.
Here is its abstract:
We can regard operations that discard information, like specializing to a particular case or dropping the intermediate steps of a proof, as projections, and operations that reconstruct information as liftings. By working with several projections in parallel we can make sense of statements like "Set is the archetypal Cartesian Closed Category", which means that proofs about CCCs can be done in the "archetypal language" and then lifted to proofs in the general setting. The method works even when our archetypal language is diagrammatical, has potential ambiguities, is not completely formalized, and does not have semantics for all terms. We illustrate the method with an example from hyperdoctrines and another from synthetic differential geometry.
This was my first "real" paper.
For my talk at the UniLog 2010 (below) I prepared a HUGE set of slides, and after chatting with several people at the conference I understood that the best way to try to publish those ideas would be to focus on the philosophical side and to leave out most technicalities (e.g., fibrations)... so I wrote "Internal Diagrams in Category Theory" and submitted it to LU. The referees told me to change some things in it, including the title, and to split the paper in two. Instead of splitting it I wrote some new sections to explain how its two "halves" were connected, and this became "Internal Diagrams and Archetypal Reasoning in Category Theory".
I abandoned the idea of "downcasings" after some years - now I use internal diagrams and particular cases. See here and here.
(2013) Internal Diagrams and
Archetypal Reasoning in Category Theory
(2010) Internal Diagrams in Category
Theory
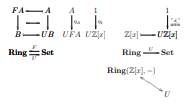
Downcasing Types (at UniLog'2010)
I gave a talk about Downcasing Types at the special session on Categorical Logic of UNILOG'2010, on 2010apr22. Very few people attended - because of the volcanic ashes many people could not fly to Portugal, and from all these programmed talks only these ended up happening. The abstract was:
When we represent a category C in a type system it becomes a 7-uple, whose first four components - class of objects, Hom, id, composition - are "structure"; the other three components are "properties", and only these last three involve equalities of morphisms.
We can define a projection that keeps the "structure" and drops the "properties" part; it takes a category and returns a "proto-category", and it also acts on functors, isos, adjunctions, proofs, etc, producing proto-functors, proto-proofs, and so on.
We say that this projection goes from the "real world" to the "syntactical world"; and that it takes a "real proof", P, of some categorical fact, and returns its "syntactical skeleton", P-. This P- is especially amenable to diagrammatic representations, because it has only the constructions from the original P --- the diagram chasings have been dropped.
We will show how to "lift" the proto-proofs of the Yoneda Lemma and of some facts about monads and about hyperdoctrines from the syntactical world to the real world. Also, we will show how each arrow in our diagrams is a term in a precise diagrammatic language, and how these diagrams can be read out as definitions. The "downcased" diagrams for hyperdoctrines, in particular, look as diagrams about Set (the archetypical hyperdoctrine), yet they state the definition of an arbitrary hyperdoctrine, plus (proto-)theorems.
A longer version of the abstract:
PDF.
First official release of the slides (2010jun21, 100 pages):
pdf.
Latest version of the slides (109 pages): dvi, pdf.
Natural infinitesimals in filter-powers (2008)
"Purely calculational proofs" involving infinitesimals can be "lifted" from the non-standard universe (an ultrapower) to the "semi-standard universe" (a filter-power) through the quotient SetI/F→SetI/U; and after they've been moved to the right filter-power they can be translated very easily to standard proofs. I don't know how much of this idea is new, but I liked it so much that I wrote it down in some detail and asked for feedback in the Categories mailing list.
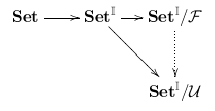
Preliminary version (2008jul13), including the message to the mailing list: pdf, dvi, source.
A (long-ish) abstract for a presentation intended for undergrads:
pdf,
source.
I presented that at the students' colloquium at
PUC-Rio, on 2008aug20, 17:00-18:00hs.
I will talk about it again at
IMPA, on
2008sep17, 15:30 (pdf).
(News: Reinhard Boerger pointed me to later (post-1958) work by Laugwitz and Schmieden, and I got a copy of the "Reuniting the Antipodes" book; my current impression is that my result is not as trivial as I was afraid it could be. Homework-in-progress: several cleanups on the preliminary version above, and I'm trying - harder - to understand Moerdijk and Palmgren's sheaf models.)
Note (2010): I still don't have the tools for formalizing this idea completely. As what I have is an "incomplete internal language", the ideas in this preprint may help.
Sheaves for Non-Categorists (2008)
This is another presentation that - maybe after some clean-ups - will be accessible to undergrads... The current version of the slides (far from ready, with lots of garbage and gaps!) is here: pdf, source. The presentation will be at the Logic Seminar at UFF, on 2008sep04, 16:00-17:00hs.
Here's an htmlized version of the abstract:
Take a set of "worlds", W, and a directed acyclical graph on W, given by a relation R ⊂ W × W. Let's call the functions W → {0,1} "modal truth-values", and the R-non-decreasing functions W → {0,1} "intuitionistic truth-values". If we see W as a topological space with the order topology induced by R, the intuitionistic truth-values correspond to open sets.
The pair (O(W), ⊆) is a Heyting algebra --- meaning that we can interpret intuitionistic propositional logic on it --- and it is a (bigger) DAG, and so we can repeat the above process with it, to generate a (bigger) topological space (O(W), O(O(W))), which is the natural setting for talking about "covers", "saturated covers", and "unions of covers".
This presentation will be focused on understanding all these ideas (and more!), mainly in the case where W has three worlds forming a "V", and R has two arrows pointing downwards. The operation of "taking the union of a cover" turns out to be a particular case of a "Lawvere-Tierney modality"; the double negation is another LT-modality.
Seminar on downcasing types (nov/2007)
If you are going to attend my seminars at PUC at November/2007 and want to take a peek at my notes (they are very incomplete at the moment, it goes without saying), they have just been split into several parts:
- 1. Downcasing Sets
- 2. Downcasing Type Systems
- 3. Downcasing the Beck-Chevalley Condition
- 4. Downcasing the Structure of a Topos
- 5. Downcasing Comprehension Categories
- 6. Notes about Hyperdoctrines
- 7. Notes about Sheaves
- 8. Downcasing ring objects of line type (as in Kock77; for SDG)
- 9. Notes about monads (and *-autonomous and differential categories)
- 10. Notes about the notation in several papers
- 11. Notes about the notation in Kock & Mikkelsen's paper on ultrapowers
Bad news (?), dec/2007: the seminars will not happen - instead, I got a job at São Paulo, on computer stuff. I'll keep working on maths and on my personal free software projects in my spare time. If you find any of these things interesting, and want to discuss or to encourage me to finish something, get in touch!
2008: I am giving a series of seminars at UFF to try to organize my ideas about downcasing types... here are links to some of TeXed slides (they are very preliminary, too. Should I be embarassed to provide links to these things? Well...):
General links
I moved them to this page.
PhD and post-PhD research *
I did both my MsC and my PhD (and also my graduation, by the way) at the Department of Mathematics at PUC-Rio. The Dept of Mathematics is a fantastic place - tiny, incredibly friendly, well-equipped, lots of research going on -, but (rant mode on) PUC-Rio is a private university, and most of the students from other departments were ultra-competitive rich kids who had never stepped out of the marble towers they live in. I used to find it very hard - very painful, even - to interact with them, and even to stand their looks, like if they were always trying to tag me as either a "winner" or a "loser", as if there weren't any other ways to live. Eeek! But these days are long gone now (rant mode off).
I spent the first eight months of 2002 at McGill University in Montreal, doing research for my PhD thesis there, working with Robert Seely... I was in a "Sandwich PhD" program (thanks CAPES!), which is something that lets us do part of the research abroad and then come back and finish (and defend) the thesis at our university of origin.
I defended my PhD thesis (with lots of holes) in August, 2003 and presented the final version - filling out some of the gaps - in February, 2004. Then I spent most of 2004 teaching part-time in an university at the outskirts of Rio (FEBF/UERJ), and also trying to finish a very important Free Software project that I've been working on since 1999 (GNU eev).
The thesis is in Portuguese and you don't want to see it. Really. =(
News (2010/2013): this paper has all the ideas from my PhD thesis, plus some! It fills all the gaps from the thesis, and it is quite well written =).
News (October 2005): I gave a series of talks about my PhD thesis at UFF.
This is the abstract for a talk that I gave at the FMCS2002 in June 8, 2002.
Title: A System of Natural Deduction for Categories
We will present a logic (system DNC) whose terms represent categories, objects, morphisms, functors, natural transformations, sets, points, and functions, and whose rules of deduction represent certain constructive operations involving those entities. Derivation trees in this system only represent the "T-part" (for "terms" and "types") of the constructions, not the "P-part" ("proofs" and "propositions"): the rules that generate functors and natural transformations do not check that they obey the necessary equations. So, we can see derivations in this system either as constructions happening in a "syntactical world", that should be related to the "real world" in some way (maybe through meta-theorems that are yet to be found), or as being just "skeletons" of the real constructions, with the P-parts having been omitted for briefness.
Even though derivations in DNC tell only half of the story, they still have a certain charm: DNC terms represent "types", but a tree represents a construction of a lambda-calculus term; there's a Curry-Howard isomorphism going on, and a tree can be a visual help for understanding how the lambda-calculus term works -- how the data flows inside a given categorical construction. Also, if we are looking for a categorical entity of a certain "type" we can try to express it as a DNC term, and then look for a DNC "deduction" having it as its "conclusion"; the deduction will give us a T-part, and we will still have to go back to the standard language to supply a P-part, but at least the search has been broken in two parts...
The way to formalize DNC, and to provide a translation between terms in its "logic" and the usual notations for Category Theory, is based on the following idea. Take a derivation tree D in the Calculus of Constructions, and erase all the contexts and all the typings that appear in it; also erase all the deduction steps that now look redundant. Call the new tree D'. If the original derivation, D, obeys some mild conditions, then it is possible to reconstruct it -- modulo exchanges and unessential weakenings in the contexts -- from D', that is much shorter. The algorithm that does the reconstruction generates as a by-product a "dictionary" that tells the type and the "minimal context" for each term that appears in D'; by extending the language that the dictionary can deal with we get a way to translate DNC terms and trees -- and also, curiously, with a few tricks more, and with some minimal information to "bootstrap" the dictionary, categorical diagrams written in a DNC-like language.
I also gave a shorter version of that talk at the CMS Summer 2002 Meeting, in June 17.
Slides for the longer talk (45 minutes, 26+3 pages): pdf, ps, dvi, source.
Slides for the shorter talk (one week later, 15 minutes, 16+2 pages: pdf, ps, dvi, source.
Fact: all the essential details (i.e., the "T-part", as in the abstract above) of a certain construction of a categorical model of the Calculus of Constructions - and also of categorical models of several fragments of CC - can be expressed in (a few!) categorical diagrams using the DNC language. I'm currently (February/March 2005) preparing talks and articles about that.
An older talk about Natural Deduction for Categories. After using something like the DNC notation for years just because "it looked right", but without any good formal justification for it, in February 2001 I had the key idea: there were rules of both discharge and introduction for the "connectives" for functors and natural transformations. A few months after that (in July 5 2001, to be precise) I gave a talk about it at a meeting called Natural Deduction Rio 2001.
Abstract (3 pages and a bit): pdf, ps, dvi, source.
Slides (16 slides): pdf, ps, dvi+eps's, source.
Another talk, even older, about Natural Deduction for Categories. After finding the key idea that I mentioned above I arranged to give a (very informal) talk at the Centro de Lógica e Epistemologia at UNICAMP. It happened in April 25, 2001, and for it I had to assemble my personal notes into something that could be used as slides. The title was ""Set^C is a topos" has a syntactical proof".
The notes from which the slides were made: ps, dvi+eps's, source.
MsC Thesis and related things *
My master's thesis: "Categorias, Filtros e Infinitesimais Naturais" (April, 1999). The thesis and the slides used in the defense are in Portuguese.
Thesis (7+116 pages): ps, pdf, dvi+eps's, source.
Slides (15 slides): ps, pdf, dvi+eps's, source.
The diagrams were made with diaglib and the deduction trees with dednat.icn.
A few months after the defense (in February 24, 2000, to be precise) I gave a talk at UFF about a kind of "Nonstandard Analysis with Filters", and about skeletons of proofs. Slides (12 slides plus one page), in Portuguese: pdf, ps, dvi+eps's, source.
My advisor at PUC: Nicolau Saldanha
Typesetting categorical diagrams in LaTeX
2017set19: update: since mid-2015 I'm using Dednat6, LuaLaTeX and pict2e for all my diagrams.
My PhD thesis included lots of hairy categorical diagrams, and I ended up writing a LaTeX preprocessor in Lua - called "dednat4.lua" - to help me typeset them. Below are some examples of diagrams that I have typeset with dednat4:
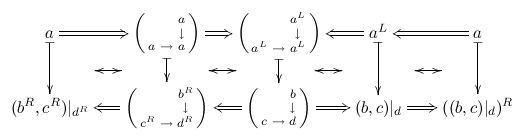
|
|||||
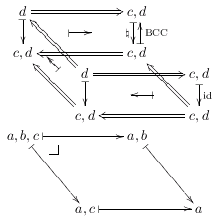
|
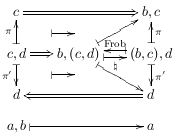
|
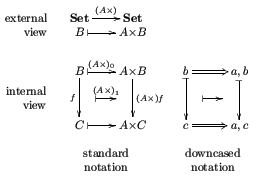
|
|||
Note that dednat4 is obsolete, and that the diagrams above use an obsolete notation - the notation for "downcasings" from IDARCT...