Optativa: Lógicas, traduções e raciocício diagramático

A ser oferecida por: Eduardo Ochs
no PURO/UFF, em 2016.1...
Título (versão humanas): "Lógicas, traduções e raciocício diagramático"
Título (versão exatas): "Lambda-cálculo, lógicas e linguagens de programação"
Código: RCN00049
Horário: terças das 16:00 às 18:00, no LLaRC (do lado da biblioteca)
No sistema a disciplina aparece com o título "versão exatas" (o que pode ser meio assustador)...
Update: estou pondo um registro de cada aula aqui.

1. Introdução (original).

Deixa eu começar explicando porque me interessa oferecer este curso...

Eu comecei a estudar Teoria de Categorias há muitos anos atrás porque me parecia ser uma área na qual as demonstrações podiam ser bem visuais, já que muita coisa era feita com diagramas... mas os livros de Categorias quase sempre tinham só descrições textuais dos diagramas, por razões técnicas das editoras, e além disso eles só descreviam em detalhes os casos mais gerais, incrivelmente abstratos, e os "exemplos motivadores", que tinham levado as pessoas a inventarem as estruturas mais abstratas, eram relegados à seção de exercícios, ou mencionados em duas linhas como se fossem óbvios...

Aos poucos eu fui desanimando de trabalhar em coisas que só poucos especialistas entenderiam e fui me empolgando por um lado mais "didático": técnicas que tornavam vários conceitos de Categorias mais acessíveis para não-especialistas. Em 2010 eu afinal consegui tapar vários buracos conceituais da minha tese de doutorado e escrever um artigo - este aqui: PDF - sobre três idéias-chave:

• podemos desenhar lado a lado os diagramas o caso geral e de um caso particular; eles vão ter a mesma forma, e compará-los nos ajuda muito a aprender sobre o caso geral,
• se encontrarmos um caso particular "arquetipal" podemos reaprender quase toda a teoria do caso geral nele,
• vários casos arquetipais importantes envolvem só objetos finitos pequenos que podem ser escritos explicitamente.

Nos últimos anos - mais ou menos de 2012 pra cá - eu praticamente parei de conviver com gente de Exatas, e tenho tentado adaptar boa parte deste material pra ele ficar acessível para pessoas de Ciências Sociais, Psicologia, etc, que se acreditam totalmente incompetentes pra Matemática. As apresentações informais que fiz pra essas pessoas (ou: "para crianças", no sentido dos slides 1.1 e 1.2 aqui) funcionaram muito bem, mas ainda não consegui organizar todo o material numa forma auto-contida, como notas de seminário com exercícios ou como um livro-texto... porque é muito difícil escrever textos grandes e detalhados sem uma motivação concreta e sem termos uma noção clara de pra quem estamos escrevendo!

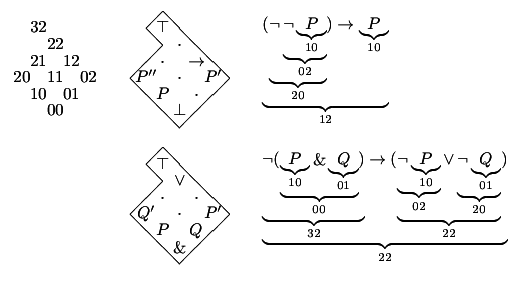
O meu objetivo principal em oferecer esta optativa é organizar esse material, principalmente as figuras que faltam (dê uma olhada nas figuras daqui: "Intuitionistic Logic for Children, or: Planar Heyting Algebras for Children") e os exercícios. Eu ando tentando interagir academicamente com pessoas de Lógica Filosófica - que andam produzindo coisas como isto, que eu achei fascinante: "Picturing Hegel" - e elas já me disseram que o meu trabalho em "Lógica pra crianças" interessa a elas muitíssimo, só falta eu conseguir escrever e publicar...

2. Introdução (IHS).

No início de março uma aluna da computação perguntou pro Fernando Naufel se ele poderia dar uma optativa em 2016.1 ("Teoria dos números e criptografia"), e ela explicou que como 2016.1 vai ser mais curto que os períodos normais as disciplinas obrigatórias de matemática e física vão ficar ainda mais pesadas, porque o mesmo conteúdo vai ter que ser dado em menos tempo, então os alunos estão de olho em optativas...

Alguns dias depois eu me toquei de eu tinha material pra dar uma optativa bem interessante, que seria sem pré-requisitos e praticamente sem deveres de casa. Aí preparei boa parte do material abaixo (formulário 13, "material de propaganda", etc) e quando discutimos na reunião do RCN de 17/março como formalizar essa optativa vimos que ela precisaria ser aprovada pelo colegiado da Computação.

Não sei se o colegiado da Computação aprovaria isso a tempo - veja este áudio de reunião, de 44:38 a 1:06:15 (está parcialmente transcrito).

Aí me ocorreu um plano B, bem mais seguro, que é formalizar o curso como uma optativa pro IHS, com um programa um pouquinho menor, sem as partes que faziam referência a programação, e tornando o curso mais adequado pra quem se interessa por Filosofia ou por Lacan.

Update: Conseguimos oficializar a optativa pelo RCN. Ela ficou com o código RCN00049 e com o título "Lambda-cálculo, lógicas e linguagens de programação", que talvez assuste algumas pessoas. Vou tentar usar o outro título - "Lógicas, traduções e raciocício diagramático" - onde der.

3. Programa (exatas).

Parte 1:
Revisão da parte sem objetos infinitos de Matemática Discreta
A calculadora da Gabriela
Regras de redução para expressões
Funções
Variáveis livres
Quantificadores, comprehension, lambda
Categorias
Set e ordens parciais são categorias
Categorias com operações extras: terminais, limites, exponenciais
ZHAs para crianças
Categorias Cartesianas Fechadas: Set e ZHAs
Lógica intuicionista para crianças (usando ZHAs)
Tautologias clássicas que não são tautologias em ZHAs
Lambda-cálculo simplesmente tipado (L1) para crianças
Como interpretar L1 em Set
Dedução Natural para crianças
Curry-Howard para crianças
Semânticas categóricas para crianças
S4 (uma lógica modal) para crianças

Parte 2:
Mini-tutoriais de três linguagens funcionais:
• Lua
• Emacs Lisp
• OCAML
Vamos examinar algumas linguagens do PLZoo.

4. Programa (humanas - preliminar).

Conjuntos e listas
Grafos direcionados
A calculadora da Gabriela
Regras de redução para expressões
Funções
Variáveis livres
Quantificadores, comprehension, lambda
Categorias
Set e ordens parciais são categorias
Categorias com operações extras: terminais, limites, exponenciais
ZHAs para crianças
Categorias Cartesianas Fechadas: Set e ZHAs
Lógica intuicionista para crianças (usando ZHAs)
Tautologias clássicas que não são tautologias em ZHAs
Lambda-cálculo simplesmente tipado (L1) para crianças
Como interpretar L1 em Set
Dedução Natural para crianças
Curry-Howard para crianças
Semânticas categóricas para crianças
S4 (uma lógica modal) para crianças

5. Sobre o método de avaliação do curso.

1) Dá pra passar com uma nota razoável só fazendo os exercícios "pra crianças" em sala.

2) Quem quiser uma nota maior pode apresentar um "seminário de decifração de livro", que consiste em apresentar pra turma um dos trechos selecionados de um dos livros - Awodey, Carnielli/Epstein, Copi, Davey/Priestley, MacLane, Marcos, etc - comparando o trecho original, que fala de algo geral e abstrato, com um caso particular.

6. Lacan.

Isto aqui é um trecho do "Seminário 17: o avesso da psicanálise", do Jacques Lacan (pags 84-85). Os itálicos são todos meus.

Eis o que, espero, não deixa de ter ressonância para vocês - sem que saibam aliás se essa ressonância vem de direita ou de esquerda. Isto se estrutura primeiro no chamado suporte mítico de certas sociedades. Podemos analisá-las como etnográficas, quer dizer, como escapando ao discurso do mestre, pelo fato de que este começa com a predominância do sujeito, na medida em que ele tende justamente a se sustentar nesse mito ultra-reduzido, o de ser idêntico a seu próprio significante.

Foi nisso que lhes indiquei da última vez o que esse discurso tem de natureza afim à da matemática, onde A representa a si mesmo, sem precisar do discurso mítico para dar-lhe suas relações. É por aí que a matemática representa o saber do mestre como constituído com base em outras leis que não as do saber místico.

Em suma, o saber do mestre se produz como um saber inteiramente autônomo do saber mítico, e isto é o que se chama de ciência.

Indiquei-lhes da última vez sua figura numa rápida evocação da termodinâmica e, indo mais longe, de toda unificação do campo físico. Esta se baseia na conservação de uma unidade que nada mais é do que uma constante, sempre reencontrada na conta - não digo sequer uma quantificação - de uma manipulação de cifras, ou seja, definida de tal modo que faça aparecer na conta, em todos os casos, essa constante. Eis o que sustenta sozinho o que é chamado, no fundamento da ciência física, de energia.

Essa sustentação provém de que a matemática só pode ser construída a partir do fato de que o significante é capaz de significar a si mesmo. O A que vocês escreveram uma vez pode ser significado por sua repetição de A. Ora, essa posição é estritamente insustentável, constitui uma infração à regra em relação à função do significante, que pode significar tudo, salvo, certamente, a si mesmo. É preciso se livrar desse postulado inicial para que o discurso matemático se inaugure.

7. Disclaimer.

Eu não tenho a menor pretensão de ensinar Lacan, Hegel, ou qualquer ou coisa de Filosofia, Ciências Sociais, etc no curso - meus conhecimentos disso são só os de um diletante animado... mas muitos dos filósofos e psicanalistas com os quais eu já conversei sentem que é muito útil entender um pouco de matemática, principalmente como em matemática nós definimos várias noções de verdade, começando com a que é tecnicamente mais simples e construindo outras a partir desta... e isto nós vamos ver no curso, em detalhes e na prática, com exercícios bacanas. =)

8. Formulários 13.

Versão computação: PDF, ODT.
Versão humanas: PDF, ODT.

9. Figuras.

(Pro Facebook ficar feliz)